- Carga de datos
- Filtrado de datos
- Representación gráfica
- Regresión lineal
- Análisis de diferencias entre grupos mediante t-student
1. CARGA DE DATOS
Descargamos el fichero de datos con el que vamos a trabajar: https://www.dropbox.com/s/lg83ut9hzwctnlp/quantitativeData.csv?dl=0. El fichero es un archivo CSV (Comma-Separated Values) en el que subyace una estructura tabulada: cada fila representa una muestra u observación (un sujeto) y cada columna representa un campo de datos; los campos de datos se separan entre sí mediante el carácter ";". Al abrir el fichero en Microsoft Excel, veremos que dicha estructura tabulada no aparece reflejada en pantalla; es decir: los diferentes campos de cada fila se muestran aglutinados dentro una celda (ver figura 1).
Para que la información se muestre correctamente en pantalla, debemos importar los datos en una nueva hoja: Asistente para importar texto. Una vez consigamos visualizar correctamente los datos (ver figura 2), revisamos su estructura y contenido: en el fichero constan los datos de 121 estudiantes, de los cuales 60 utilizaron un entorno Moodle y 61 utilizaron un entorno PLE. Entre esos datos figuran la calificación final y el tamaño de la red personal de cada estudiante.
Los siguientes pasos van dirigidos a la obtención de una figura en la que se representen las calificaciones de los estudiantes (campo "grade" de la variable "quantitativeData") en función del tamaño de sus redes personales (campo "egonet_size" de la variable "quantitativeData"). Asimismo, se representarán las líneas de tendencia que relacionan las calificaciones de los estudiantes con el tamaño de sus redes personales. En dicha figura se diferenciarán, mediante distintos colores, los estudiantes que utilizaron el entorno Moodle de los que utilizaron el entorno PLE.
2. FILTRADO DE DATOS
Para filtrar los sujetos por tipo entorno, escribimos los siguientes comandos en la consola:
Las líneas se deben leer de derecha a izquierda, es decir, el resultado del comando "subset()" se carga en una nueva variable ("datosMoodle" o "datosPLE"). Dentro del comando "subset()", se indican diferentes parámetros (ver documentación: https://www.rdocumentation.org/packages/base/versions/3.4.3/topics/subset):
Al ejecutar estos comandos, se crearán dos nuevas variables: "datosMoodle" (60 observaciones) y "datosPLE" (61 observaciones). Podemos seleccionar dichas variables a través de la cuadrícula superior derecha e inspeccionar el contenido de dichas variables a través de la cuadrícula superior izquierda (ver figura 6). Esta operación equivale a ejecutar el comando "View()" en la consola.
En primer lugar, debemos crear el "marco" sobre el que representar los puntos (los sujetos, en este caso, estudiantes). Para ello, es necesario definir unos ejes X e Y cuya longitud abarque el rango de valor de las variables que se desea representar (la calificación final y el tamaño de la red personal de cada estudiante). Para ello, introducimos el siguiente comando:
Al comando "plot()" se le pasan 5 parámetros de acuerdo a lo indicado en su documentación (https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/plot):
NOTA. Qué es un vector de datos: https://es.wikipedia.org/wiki/Vector_(inform%C3%A1tica)
El marco de la gráfica se muestra en la cuadrícula inferior derecha, la cual se puede maximizar (ver figura 7).
Al comando "points()" se le pasan 4 parámetros de acuerdo a lo indicado en su documentación (https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/points):
En lugar de introducir los dos vectores de coordenadas de forma separada, también podemos introducir los datos en formato y=f(x), es decir, "grade" (variable dependiente) es función de "egonet_size" (variable independiente).
A partir de la observación de las distribuciones de puntos de cada grupo, podemos inferir que conforme aumenta el tamaño de la red personal de los estudiantes, también lo hace la calificación final obtenida por éstos. Para confirmar esta observación, procedemos a ajustar cada una de las distribuciones de puntos con una recta mediante una regresión lineal simple.
4. REGRESIÓN LINEAL
Una regresión lineal simple es un procedimiento estadístico para generar los coeficientes de un modelo (en este caso, una recta y = B1*x + B0) que relaciona una variable respuesta (y, en este caso, la calificación final) con una variable predictora (x, en este caso, el tamaño de red). El comando "lm()" permite calcular los parámetros del modelo (B1 y B0):
No obstante, de acuerdo con la documentación del comando "lm()" (https://www.rdocumentation.org/packages/stats/versions/3.4.3/topics/lm), los datos también se podían haber introducido de la siguiente forma:
Analizemos los resultados obtenidos (ver figura 9): la recta de mejor ajuste para relacionar "grade" y "egonet_size" de los estudiantes que utilizaron Moodle es y = 1.96x + 45.17 y la de los estudiantes que utilizaron el PLE es y = 1.041x + 40.956.
Ahora analizamos la significancia ESTADÍSTICA de estos coeficientes en cada uno de los modelos, es decir, cómo de bueno es el ajuste de cada recta (ver figura 10).
El texto que escribiríamos en un artículo en el que publicáramos los resultados sería el mostrado en la Tabla 1.
Table 1. Estimates of the simple linear regressions (y = B1*x + B0) calculated to observe the trend of the grade (dependent variable, y) over the egonet size (independent variable, x). A significant regression equation was found in Moodle ( F(1, 58) = 20.89, p < 0.001 ), with an R2 of 0.2648. A significant regression equation was found in PLE ( F(1, 59) = 56.46, p < 0.001 ), with an R2 of 0.489.
NOTA: R2 (R cuadrado) se define como la proporción de la varianza total explicada por la regresión; es decir, es una medida de la bondad del ajuste del modelo y = B1*x + B0.
Finalmente, representamos cada una de las rectas sobre la gráfica utilizando el comando "abline()", al cual se le pasan como parámetros los coeficientes de la recta, así como el color y el grosor que se desean utilizar para dibujarla (ver documentación: https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/abline). La figura 11 muestra el resultado final.
5. ANÁLISIS DE DIFERENCIAS ENTRE GRUPOS MEDIANTE t-student
En la figura anterior, podemos observar que la nube de puntos correspondiente al grupo de estudiantes que utilizó el entorno PLE tiene una calificación final y un tamaño de red personal mayor que el grupo de estudiantes que utilizó el entorno Moodle. Calculamos la medias para hacernos una idea de la medida en que dichos indicadores varían entre ambos grupos.
Media de la calificación final en cada grupo:
Por lo tanto, un estudiante que utilizó el entorno PLE obtuvo, de media, 3.7 ptos más (sobre 100) que un estudiante que utilizó el entorno Moodle. Desde un punto de vista subjetivo, no parece una diferencia significativa.
Media del tamaño de red personal en cada grupo:
Por lo tanto, la red personal de un estudiante que utilizó el entorno PLE es 2.5 veces más grande que la red de un estudiante que utilizó el entorno Moodle. Desde un punto de vista subjetivo, sí que parece una diferencia significativa.
Además de esta percepción acerca de las diferencias basada en las medias, también nos interesa conocer en qué medida las diferencias observadas entre grupos se deben o no al azar, porque ello nos permitirá saber si el entorno de aprendizaje es una variable explicativa a la hora de que los estudiantes obtengan mejores calificaciones y establezcan redes personales de mayor tamaño. Es decir, queremos saber si las diferencias observadas entre grupos en la calificación final y el tamaño de red personal son ESTADISTICAMENTE significativas.
La t de student es un tipo de test estadístico que analiza la influencia de una variable categórica independiente de dos categorías sobre una variable continua dependiente. La t de student es un test paramétrico, lo cual significa que su procedimiento se basa en el análisis de un determinado parámetro estadístico (la media) a partir del conocimiento de la distribución que siguen los datos (una distribución normal). Cuando no se conoce la distribución que siguen los datos, entonces se utilizan test no paramétricos cuyo procedimiento se basa en analizar los datos en sí mismos, sin asociarlos a ninguna distribución. Mientras que los test paramétricos se utilizan con variables continuas como variables dependientes, los test no paramétricos se suelen utilizar con variables ordinales (por ejemplo, una escala Likert de un cuestionario) como variables dependientes.
Figura 1. Visualización de los datos al abrir directamente el fichero CSV con Excel.
Para que la información se muestre correctamente en pantalla, debemos importar los datos en una nueva hoja: Asistente para importar texto. Una vez consigamos visualizar correctamente los datos (ver figura 2), revisamos su estructura y contenido: en el fichero constan los datos de 121 estudiantes, de los cuales 60 utilizaron un entorno Moodle y 61 utilizaron un entorno PLE. Entre esos datos figuran la calificación final y el tamaño de la red personal de cada estudiante.
Figura 2. Visualización de los datos después de haber utilizado el Asistente para importar texto.
Una vez hemos revisado los datos y nos hemos familiarizado con su estructura, abrimos la interfaz
R studio y procedemos a cargar el fichero de datos en una variable (data frame) con la que operaremos en R. Para ello, seleccionamos las siguientes opciones en el menú de la cuadrícula superior derecha: Import Dataset → From text file (ver figura 3).
A continuación, se abre una ventana en cuya parte derecha se muestra, por un lado, el contenido del fichero de texto y, por otro lado, la estructura de datos que se va a cargar en una variable a partir de dicho contenido según las opciones indicadas en la parte izquierda de ventana. Para que la creación de la variable se realice de forma correcta, debemos indicar, a través de dichas opciones, si el contenido del fichero de datos incluye una cabecera, cuál es el separador utilizado entre variables, cuál es el carácter utilizado para separar la parte entera de la parte decimal de un número, etc. Este proceso es interactivo, de manera que, según vamos cambiando las opciones, se va actualizando la estructura de la variable. Entre las opciones disponibles, también se incluye el nombre con el que se desea identificar la variable (ver figura 4).
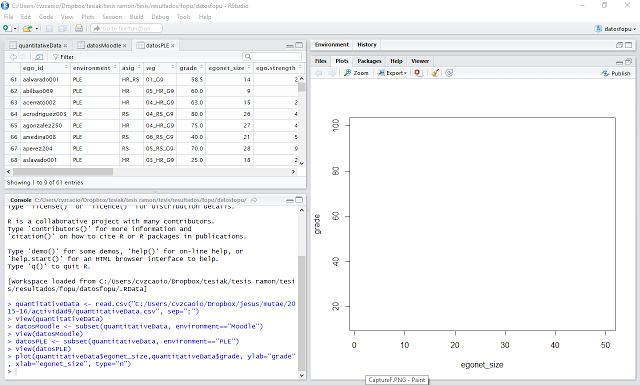
Si el proceso se completa correctamente, la estructura de datos debería aparecer representada de forma tabulada en la cuadrícula superior izquierda. De esta forma, el entorno de trabajo de RStudio queda compuesto de 4 cuadrículas (ver figura 5):
NOTA: en la figura 5 también podemos observar que el proceso asociado al asistente de carga de datos se traduce en la introducción automática de un comando en la consola ( read.csv() ), con sus correspondientes opciones.
Figura 3. Primer paso para cargar el fichero de datos en una variable.
A continuación, se abre una ventana en cuya parte derecha se muestra, por un lado, el contenido del fichero de texto y, por otro lado, la estructura de datos que se va a cargar en una variable a partir de dicho contenido según las opciones indicadas en la parte izquierda de ventana. Para que la creación de la variable se realice de forma correcta, debemos indicar, a través de dichas opciones, si el contenido del fichero de datos incluye una cabecera, cuál es el separador utilizado entre variables, cuál es el carácter utilizado para separar la parte entera de la parte decimal de un número, etc. Este proceso es interactivo, de manera que, según vamos cambiando las opciones, se va actualizando la estructura de la variable. Entre las opciones disponibles, también se incluye el nombre con el que se desea identificar la variable (ver figura 4).
Figura 4. Configuración de las opciones de carga del fichero CSV.
Si el proceso se completa correctamente, la estructura de datos debería aparecer representada de forma tabulada en la cuadrícula superior izquierda. De esta forma, el entorno de trabajo de RStudio queda compuesto de 4 cuadrículas (ver figura 5):
- La cuadrícula superior derecha se utiliza para cargar datos, visualizar las variables de trabajo y ver el histórico de comandos.
- La cuadrícula superior izquierda se utiliza para visualizar el contenido de las variables.
- La cuadrícula inferior izquierda se utiliza para introducir los comandos que permiten procesar y analizar los datos; es decir, esta cuadrícula es la consola o terminal de R.
- La cuadrícula inferior derecha se utilizar para visualizar gráficas.
NOTA: en la figura 5 también podemos observar que el proceso asociado al asistente de carga de datos se traduce en la introducción automática de un comando en la consola ( read.csv() ), con sus correspondientes opciones.
Figura 5. Entorno de trabajo compuesto de 4 cuadrículas.
Los siguientes pasos van dirigidos a la obtención de una figura en la que se representen las calificaciones de los estudiantes (campo "grade" de la variable "quantitativeData") en función del tamaño de sus redes personales (campo "egonet_size" de la variable "quantitativeData"). Asimismo, se representarán las líneas de tendencia que relacionan las calificaciones de los estudiantes con el tamaño de sus redes personales. En dicha figura se diferenciarán, mediante distintos colores, los estudiantes que utilizaron el entorno Moodle de los que utilizaron el entorno PLE.
Para filtrar los sujetos por tipo entorno, escribimos los siguientes comandos en la consola:
datosMoodle <- subset(quantitativeData, environment=="Moodle")
datosPLE <- subset(quantitativeData, environment=="PLE")
Las líneas se deben leer de derecha a izquierda, es decir, el resultado del comando "subset()" se carga en una nueva variable ("datosMoodle" o "datosPLE"). Dentro del comando "subset()", se indican diferentes parámetros (ver documentación: https://www.rdocumentation.org/packages/base/versions/3.4.3/topics/subset):
- El primero indica la variable que actua como fuente de datos: "quantitativeData".
- El segundo indica el filtro o la condición a aplicar a la fuente de datos: en el primer caso, deseamos quedarnos con aquellas observaciones (filas) que cumplan que el campo "environment" (columna) es igual a la cadena de texto "Moodle".
Al ejecutar estos comandos, se crearán dos nuevas variables: "datosMoodle" (60 observaciones) y "datosPLE" (61 observaciones). Podemos seleccionar dichas variables a través de la cuadrícula superior derecha e inspeccionar el contenido de dichas variables a través de la cuadrícula superior izquierda (ver figura 6). Esta operación equivale a ejecutar el comando "View()" en la consola.
Figura 6. Seleccionar las nuevas variables y examinar su contenido.
3. REPRESENTACIÓN GRÁFICAEn primer lugar, debemos crear el "marco" sobre el que representar los puntos (los sujetos, en este caso, estudiantes). Para ello, es necesario definir unos ejes X e Y cuya longitud abarque el rango de valor de las variables que se desea representar (la calificación final y el tamaño de la red personal de cada estudiante). Para ello, introducimos el siguiente comando:
plot(quantitativeData$egonet_size, quantitativeData$grade, xlab="egonet_size", ylab="grade", type="n")
Al comando "plot()" se le pasan 5 parámetros de acuerdo a lo indicado en su documentación (https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/plot):
- Vector de datos X: coordenadas X de las observaciones ("egonet_size")
- Vector de datos Y: coordenadas Y de las observacioens ("grade")
- xlab: leyenda del eje X.
- ylab: leyenda del eje Y.
- type: tipo de gráfico: en este caso, el valor "n" indica "vacío".
variable_de_datosDOLARcampo_de_datos
ejemplo: quantitativeData$grade
NOTA. Qué es un vector de datos: https://es.wikipedia.org/wiki/Vector_(inform%C3%A1tica)
El marco de la gráfica se muestra en la cuadrícula inferior derecha, la cual se puede maximizar (ver figura 7).
Figura 7. Marco de la gráfica dentro del cual se represetarán los puntos.
A continuación, dibujamos los puntos que representan a los estudiantes de cada grupo (Moodle y PLE) sobre esos ejes. Para ello, utilizamos el comando "points()":
points(datosMoodle$egonet_size, datosMoodle$grade, col="blue", cex=0.9) points(datosPLE$egonet_size, datosPLE$grade, col="red", cex=0.9)
Al comando "points()" se le pasan 4 parámetros de acuerdo a lo indicado en su documentación (https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/points):
- El vector de coordenadas X de las observaciones ("egonet_size").
- El vector de coordenadas Y de las observaciones ("grade").
- col: el color de los puntos.
- cex: el tamaño de los puntos.
Figura 8. Representación de los datos dentro del marco de la gráfica.
En lugar de introducir los dos vectores de coordenadas de forma separada, también podemos introducir los datos en formato y=f(x), es decir, "grade" (variable dependiente) es función de "egonet_size" (variable independiente).
points(datosMoodle$grade ~ datosMoodle$egonet_size, col="blue", cex=0.9) points(datosPLE$grade ~ datosPLE$egonet_size, col="red", cex=0.9)
4. REGRESIÓN LINEAL
Una regresión lineal simple es un procedimiento estadístico para generar los coeficientes de un modelo (en este caso, una recta y = B1*x + B0) que relaciona una variable respuesta (y, en este caso, la calificación final) con una variable predictora (x, en este caso, el tamaño de red). El comando "lm()" permite calcular los parámetros del modelo (B1 y B0):
lmMoodle <- lm(datosMoodle$grade ~ datosMoodle$egonet_size)
lmPLE <- lm(datosPLE$grade ~ datosPLE$egonet_size)
No obstante, de acuerdo con la documentación del comando "lm()" (https://www.rdocumentation.org/packages/stats/versions/3.4.3/topics/lm), los datos también se podían haber introducido de la siguiente forma:
lmMoodle <- lm(grade ~ egonet_size, datosMoodle, col="blue", cex=0.9) lmPLE <- lm(grade ~ egonet_size, datosPLE, col="red", cex=0.9)
Analizemos los resultados obtenidos (ver figura 9): la recta de mejor ajuste para relacionar "grade" y "egonet_size" de los estudiantes que utilizaron Moodle es y = 1.96x + 45.17 y la de los estudiantes que utilizaron el PLE es y = 1.041x + 40.956.
Figura 9. Resultados de la regresión lineal.
Ahora analizamos la significancia ESTADÍSTICA de estos coeficientes en cada uno de los modelos, es decir, cómo de bueno es el ajuste de cada recta (ver figura 10).
Figura 10. Análisis estadístico del ajuste de las rectas.
El texto que escribiríamos en un artículo en el que publicáramos los resultados sería el mostrado en la Tabla 1.
Table 1. Estimates of the simple linear regressions (y = B1*x + B0) calculated to observe the trend of the grade (dependent variable, y) over the egonet size (independent variable, x). A significant regression equation was found in Moodle ( F(1, 58) = 20.89, p < 0.001 ), with an R2 of 0.2648. A significant regression equation was found in PLE ( F(1, 59) = 56.46, p < 0.001 ), with an R2 of 0.489.
NOTA: R2 (R cuadrado) se define como la proporción de la varianza total explicada por la regresión; es decir, es una medida de la bondad del ajuste del modelo y = B1*x + B0.
Finalmente, representamos cada una de las rectas sobre la gráfica utilizando el comando "abline()", al cual se le pasan como parámetros los coeficientes de la recta, así como el color y el grosor que se desean utilizar para dibujarla (ver documentación: https://www.rdocumentation.org/packages/graphics/versions/3.4.3/topics/abline). La figura 11 muestra el resultado final.
abline(lmMoodle, col="blue", lwd=2) abline(lmPLE, col="red", lwd=2)
Figura11. Representación de las rectas de regresión dentro del marco de la gráfica.
5. ANÁLISIS DE DIFERENCIAS ENTRE GRUPOS MEDIANTE t-student
En la figura anterior, podemos observar que la nube de puntos correspondiente al grupo de estudiantes que utilizó el entorno PLE tiene una calificación final y un tamaño de red personal mayor que el grupo de estudiantes que utilizó el entorno Moodle. Calculamos la medias para hacernos una idea de la medida en que dichos indicadores varían entre ambos grupos.
Media de la calificación final en cada grupo:
with(quantitativeData, tapply(grade, list(environment), mean))
Moodle PLE 64.67500 68.36885
Por lo tanto, un estudiante que utilizó el entorno PLE obtuvo, de media, 3.7 ptos más (sobre 100) que un estudiante que utilizó el entorno Moodle. Desde un punto de vista subjetivo, no parece una diferencia significativa.
Media del tamaño de red personal en cada grupo:
with(quantitativeData, tapply(egonet_size, list(environment), mean))
Moodle PLE 9.95000 26.32787
Por lo tanto, la red personal de un estudiante que utilizó el entorno PLE es 2.5 veces más grande que la red de un estudiante que utilizó el entorno Moodle. Desde un punto de vista subjetivo, sí que parece una diferencia significativa.
Además de esta percepción acerca de las diferencias basada en las medias, también nos interesa conocer en qué medida las diferencias observadas entre grupos se deben o no al azar, porque ello nos permitirá saber si el entorno de aprendizaje es una variable explicativa a la hora de que los estudiantes obtengan mejores calificaciones y establezcan redes personales de mayor tamaño. Es decir, queremos saber si las diferencias observadas entre grupos en la calificación final y el tamaño de red personal son ESTADISTICAMENTE significativas.
La t de student es un tipo de test estadístico que analiza la influencia de una variable categórica independiente de dos categorías sobre una variable continua dependiente. La t de student es un test paramétrico, lo cual significa que su procedimiento se basa en el análisis de un determinado parámetro estadístico (la media) a partir del conocimiento de la distribución que siguen los datos (una distribución normal). Cuando no se conoce la distribución que siguen los datos, entonces se utilizan test no paramétricos cuyo procedimiento se basa en analizar los datos en sí mismos, sin asociarlos a ninguna distribución. Mientras que los test paramétricos se utilizan con variables continuas como variables dependientes, los test no paramétricos se suelen utilizar con variables ordinales (por ejemplo, una escala Likert de un cuestionario) como variables dependientes.
Comparar 2 grupos
|
Comparar >2 grupos
|
|
Método paramétrico
|
t de student
|
ANOVA
|
Método NO paramétrico
|
Mann-Whitney
|
Kruskal-Wallis
|
Ejemplos de uso en bibliografía:
- t-student: Casquero, O., Ovelar, R., Romo, J., & Benito, M. (2015). Reviewing the differences in size, composition and structure between the personal networks of high- and lowperforming students. British Journal of Educational Technology, 46(1), 16-31. doi:10.1111/bjet.12110
- Mann-Whitney: Dawson, S. (2010). “Seeing” the learning community: An exploration of the development of a resource for monitoring online student networking. British Journal of Educational Technology, 41(5), 736–752. doi:10.1111/j.1467-8535.2009.00970.x
- Kruskal-Wallis: Cabero-Almenara, J., & Marín-Díaz, V. (2014). Educational Possibilities of Social Networks and Group Work. University Students’ Perceptions. Comunicar, 21(42), 2–8. doi:10.3916/C42-2014-16
NOTA. El test se puede realizar sobre muestras independientes (una observación
sobre dos grupos separados) o sobre muestras dependientes (dos observaciones
sobre el mismo grupo).
A continuación, ejecutamos el comando para realizar el test de t de student. Tal y como se puede observar, el primer parámetro se corresponde con las calificaciones del subconjunto de datos correspondiente al grupo de estudiantes de Moodle, mientras que el segundo parámetro se corresponde con las calificaciones del subconjunto de datos correspondiente al grupo de estudiantes del PLE.
Obtenemos los resultados del análisis:
t.test(datosMoodle$grade, datosPLE$grade)
Obtenemos los resultados del análisis:
¿Qué nos indican
los resultados? En primer lugar, que la media de la variable x (datosMoodle$grade)
es de 64.675, mientras que la variable y (datosPLE$grade) tiene una media de 68.36885. Por tanto, como hemos dicho anteriormente, la diferencia entre ambos grupos no parece significativa porque es es tan sólo de 3.7 ptos sobre 100; pero... ¿es esta
diferencia ESTADISTICAMENTE significativa? Es decir, ¿la diferencia se debe al factor
diferencial entre ambos grupos (el tipo de plataforma utilizada, es decir, Moodle vs PLE) o se debe al azar? Para saberlo, nos fijamos en
el p-value. ¿Qué indica el p-value?
Indica el riesgo a equivocarnos al afirmar "Sí, existe una diferencia
estadísticamente significativa entre ambos grupos debida al factor diferencial
entre dichos grupos", cuando en realidad dicha diferencia no se debe al
factor diferencial entre grupos, sino al azar. En este caso, el riesgo es de un 23.63% (p-value = 0.2363). Pero... ¿cuál
es el umbral de riesgo? 0.05 → 5%
- Si p-value < 0.05, o lo que es lo mismo, < 5% --> riesgo a equivocarnos pequeño; por ejemplo, p-value = 0.00345 (0.345%) --> OK
- Si p-value > 0.05, o lo que es lo mismo, > 5% --> riesgo a equivocarnos grande; por ejemplo, p-value = 0.0645 (6.45%) --> NO OK
- en este estudio concreto no percibimos una diferencia significativa entre los valores de las medias de cada grupo.
- la diferencia entre las calificaciones de los estudiantes de uno y otro grupo no es estadísticamente significativa.
Repetimos el test de t-student con el indicador tamaño de red personal:
t.test(datosMoodle$egonet_size, datosPLE$egonet_size)
En este caso, p-value = 7.965e-16 = 0.0000000000000007965 → 0.00000000000007965%
Por tanto, en lo que respecta al tamaño de red personal concluimos que:
- en este estudio concreto percibimos una diferencia significativa entre los valores de las medias de cada grupo.
- la diferencia entre las calificaciones de los estudiantes de uno y otro grupo es estadísticamente significativa.
A t-test revealed a significant difference between the personal network size of VLE and iPLE students. The results indicate that students using the iPLE developed larger personal networks than the students using the VLE. On the other hand, a t-test did not reveal a significant difference between the academic performance of VLE and iPLE students (Table 4).
Manual de consulta:















Hola soy Wagner Abreu, estudiante del master del otro año, casi terminando. Estupenda explicación profesores. Me interesa mucho este programa estadistico para mi trabajo de TFM. Gracias a Oskar y Jesús por todo.
ResponderEliminar